2012白银中考数学_白银中考数学试卷2023答案

1.08年中考数学压轴题，物理电学题，英语试卷

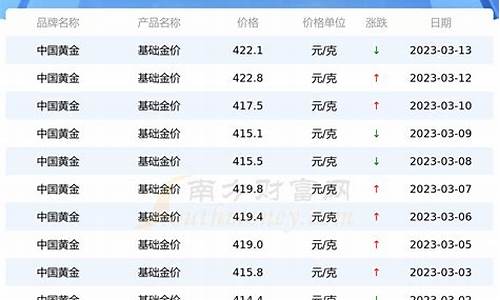
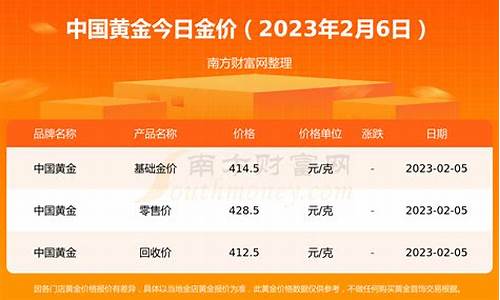
800分。通过白银教育局公布中考信息公告，得知语文、数学、英语各150分，物理、化学合卷150分，讲德取法制、史乘、地舆、生物为合卷150分，体育取强健50分，因此甘肃白银中考总分800分，中考是检验初中毕业生是否达到初中毕业水平的考试，是初中毕业证发放的必要条件。

08年中考数学压轴题，物理电学题，英语试卷

2023白银中考考试时间为6月16日-6月18日。

具体安排为:6月16日上午9:00-11:30语文、6月16日下午15:00-17:30理化综合、6月17日上午9:00-11:00数学、6月17日下午15:00-17:30道史地生综合、6月18日上午9:00-11:00英语、6月18日下午15:00-15:40体育与健康(特殊考生)。

中考数学、化学是提分最快的科目，孩子中考数学只要基础有点，计算能力不是太差，那么考个70分到80分不难，需要就是一些套路和题目的解答技巧，而化学科目相对于物理科目来说，没有那么大的难度。

是不是感觉数学都能考满分的同学，连书都不用看，其实数学学霸更重视基础。数学公式，几何图形的性质，函数的性质等，都是数学学习的基础，甚至可以说基础的好坏，直接决定中考数学成绩的高低。

在所有科目中，数学这个科目最重要错题本学习法。特别提倡大家整理错题，对于错题本有一些小窍门，那就是平时如果坚持整理错题，最终会导致自己错题本很多很厚，我们可以定期复习，对于一些彻底掌握的，可以做个标记，以后就不用再次复习，这样错题本使用起来就会效率更高。

数学学习要大量做题去巩固，但做题不要只讲究数量，更要讲究质量，遇到经典题，综合性高的题目时，每道题写完解答过程后，需要进行分析和反思，多问几个为什么，这样才能把题真正做透。

在平时学习过程中，他会把错题整理到一个错题本上。首次整理错题的时候，他会把错题的方方面面研究透彻，做到知其然知其所以然。错题本上的题他会经常复习翻看，每次考试之前再把错题本看一次，提醒自己考试当中遇到同种类型题时用正确的做题方法。

初三的时间是非常紧的，尤其是到了初三后期，初三学生恨不得把一天当成两天用。但是在这种情形下，还是有很多初三学生自习课不知道做什么，东瞅瞅西看看，结果浪费了大把时间。中考状元是不会浪费时间的，因为他们会做。他们提前把每天要做的事列出来，合理安排学习时间，提高学习效率。

2008年全国中考数学压轴题精选1

1.（08福建莆田）26．（14分）如图：抛物线经过A（-3，0）、B（0，4）、C（4，0）三点.

（1） 求抛物线的解析式.

（2）已知AD = AB（D在线段AC上），有一动点P从点A沿线段AC以每秒1个单位长度的速度移动；同时另一个动点Q以某一速度从点B沿线段BC移动，经过t 秒的移动，线段PQ被BD垂直平分，求t的值；

（3）在（2）的情况下，抛物线的对称轴上是否存在一点M，使MQ+MC的值最小？若存在，请求出点M的坐标；若不存在，请说明理由。

（注：抛物线 的对称轴为 ）

（08福建莆田26题解析）26（1）解法一：设抛物线的解析式为y = a (x +3 )(x - 4)

因为B（0，4）在抛物线上，所以4 = a ( 0 + 3 ) ( 0 - 4 )解得a= -1/3

所以抛物线解析式为

解法二：设抛物线的解析式为 ，

依题意得：c=4且 解得

所以 所求的抛物线的解析式为

（2）连接DQ，在Rt△AOB中，

所以AD=AB= 5，AC=AD+CD=3 + 4 = 7，CD = AC - AD = 7 – 5 = 2

因为BD垂直平分PQ，所以PD=QD，PQ⊥BD，所以∠PDB=∠QDB

因为AD=AB，所以∠ABD=∠ADB，∠ABD=∠QDB，所以DQ‖AB

所以∠CQD=∠CBA。∠CDQ=∠CAB，所以△CDQ∽ △CAB

即

所以AP=AD – DP = AD – DQ=5 – = ，

所以t的值是

（3）答对称轴上存在一点M，使MQ+MC的值最小

理由：因为抛物线的对称轴为

所以A（- 3，0），C（4，0）两点关于直线 对称

连接AQ交直线 于点M，则MQ+MC的值最小

过点Q作QE⊥x轴，于E，所以∠QED=∠BOA=900

DQ‖AB，∠ BAO=∠QDE， △DQE ∽△ABO

即

所以QE= ，DE= ，所以OE = OD + DE=2+ = ，所以Q（ ， ）

设直线AQ的解析式为

则 由此得

所以直线AQ的解析式为 联立

由此得 所以M

则：在对称轴上存在点M ，使MQ+MC的值最小。

2.（08甘肃白银等9市）28．（12分）如图20，在平面直角坐标系中，四边形OABC是矩形，点B的坐标为（4，3）．平行于对角线AC的直线m从原点O出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线m与矩形OABC的两边分别交于点M、N，直线m运动的时间为t（秒）．

(1) 点A的坐标是__________，点C的坐标是__________；

(2) 当t= 秒或 秒时，MN= AC；

(3) 设△OMN的面积为S，求S与t的函数关系式；

(4) 探求(3)中得到的函数S有没有最大值？若有，求出最大值；若没有，要说明理由．

（08甘肃白银等9市28题解析）28． 本小题满分12分

解：(1)（4，0），（0，3）； 2分

(2) 2，6； 4分

(3) 当0＜t≤4时，OM=t．

由△OMN∽△OAC，得 ，

∴ ON= ，S= ． 6分

当4＜t＜8时，

如图，∵ OD=t，∴ AD= t-4．

方法一：

由△DAM∽△AOC，可得AM= ，∴ BM=6- ． 7分

由△BMN∽△BAC，可得BN= =8-t，∴ CN=t-4． 8分

S=矩形OABC的面积-Rt△OAM的面积- Rt△MBN的面积- Rt△NCO的面积

=12- - （8-t）（6- ）-

= ． 10分

方法二：

易知四边形ADNC是平行四边形，∴ CN=AD=t-4，BN=8-t． 7分

由△BMN∽△BAC，可得BM= =6- ，∴ AM= ． 8分

以下同方法一．

(4) 有最大值．

方法一：

当0＜t≤4时，

∵ 抛物线S= 的开口向上，在对称轴t=0的右边， S随t的增大而增大，

∴ 当t=4时，S可取到最大值 =6； 11分

当4＜t＜8时，

∵ 抛物线S= 的开口向下，它的顶点是（4，6），∴ S＜6．

综上，当t=4时，S有最大值6． 12分

方法二：

∵ S=

∴ 当0＜t＜8时，画出S与t的函数关系图像，如图所示． 11分

显然，当t=4时，S有最大值6． 12分

说明：只有当第（3）问解答正确时，第（4）问只回答“有最大值”无其它步骤，可给1分；否则，不给分．

3.（08广东广州）25、（2008广州）（14分）如图11，在梯形ABCD中，AD‖BC，AB=AD=DC=2cm，BC=4cm，在等腰△PQR中，∠QPR=120°，底边QR=6cm，点B、C、Q、R在同一直线l上，且C、Q两点重合，如果等腰△PQR以1cm/秒的速度沿直线l箭头所示方向匀速运动，t秒时梯形ABCD与等腰△PQR重合部分的面积记为S平方厘米

（1）当t=4时，求S的值

（2）当 ，求S与t的函数关系式，并求出S的最大值

（08广东广州25题解析）25．（1）t＝4时,Q与B重合，P与D重合，

重合部分是 ＝

4.（08广东深圳）22．如图9，在平面直角坐标系中，二次函数 的图象的顶点为D点，与y轴交于C点，与x轴交于A、B两点， A点在原点的左侧，B点的坐标为（3，0），

OB＝OC ，tan∠ACO＝ ．

（1）求这个二次函数的表达式．

（2）经过C、D两点的直线，与x轴交于点E，在该抛物线上是否存在这样的点F，使以点A、C、E、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．

（3）若平行于x轴的直线与该抛物线交于M、N两点，且以MN为直径的圆与x轴相切，求该圆半径的长度．

（4）如图10，若点G（2，y）是该抛物线上一点，点P是直线下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.

（08广东深圳22题解析）22．（1）方法一：由已知得：C（0，－3），A（－1，0） …1分

将A、B、C三点的坐标代入得 ……………………2分

解得： ……………………3分

所以这个二次函数的表达式为： ……………………3分

方法二：由已知得：C（0，－3），A（－1，0） ………………………1分

设该表达式为： ……………………2分

将C点的坐标代入得： ……………………3分

所以这个二次函数的表达式为： ……………………3分

（注：表达式的最终结果用三种形式中的任一种都不扣分）

（2）方法一：存在，F点的坐标为（2，－3） ……………………4分

理由：易得D（1，－4），所以直线CD的解析式为：

∴E点的坐标为（－3，0） ……………………4分

由A、C、E、F四点的坐标得：AE＝CF＝2，AE‖CF

∴以A、C、E、F为顶点的四边形为平行四边形

∴存在点F，坐标为（2，－3） ……………………5分

方法二：易得D（1，－4），所以直线CD的解析式为：

∴E点的坐标为（－3，0） ………………………4分

∵以A、C、E、F为顶点的四边形为平行四边形

∴F点的坐标为（2，－3）或（―2，―3）或（－4，3）

代入抛物线的表达式检验，只有（2，－3）符合

∴存在点F，坐标为（2，－3） ………………………5分

（3）如图，①当直线MN在x轴上方时，设圆的半径为R（R>0），则N（R+1，R），

代入抛物线的表达式，解得 …………6分

②当直线MN在x轴下方时，设圆的半径为r（r>0），

则N（r+1，－r），

代入抛物线的表达式，解得 ………7分

∴圆的半径为 或 ． ……………7分

（4）过点P作y轴的平行线与交于点Q，

易得G（2，－3），直线为 ．……………8分

设P（x， ），则Q（x，－x－1），PQ ．

……………………9分

当 时，△APG的面积最大

此时P点的坐标为 ， ． ……………………10分

5.（08贵州贵阳）25．（本题满分12分）(本题暂无答案)

某宾馆客房部有60个房间供游客居住，当每个房间的定价为每天200元时，房间可以住满．当每个房间每天的定价每增加10元时，就会有一个房间空闲．对有游客入住的房间，宾馆需对每个房间每天支出20元的各种费用．

设每个房间每天的定价增加 元．求：

（1）房间每天的入住量 （间）关于 （元）的函数关系式．（3分）

（2）该宾馆每天的房间收费 （元）关于 （元）的函数关系式．（3分）

（3）该宾馆客房部每天的利润 （元）关于 （元）的函数关系式；当每个房间的定价为每天多少元时， 有最大值？最大值是多少？（6分）

6.（08湖北恩施）六、(本大题满分12分)

24. 如图11，在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起，A为公共顶点，∠BAC=∠F=90°，它们的斜边长为2，若?ABC固定不动，?AFG绕点A旋转，AF、与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m，CD=n.

（1）请在图中找出两对相似而不全等的三角形，并选取其中一对进行证明.

（2）求m与n的函数关系式，直接写出自变量n的取值范围.

（3）以?ABC的斜边BC所在的直线为x轴，BC边上的高所在的直线为y轴，建立平面直角坐标系(如图12).在边BC上找一点D，使BD=CE，求出D点的坐标，并通过计算验证BD ＋CE =DE .

（4）在旋转过程中,(3)中的等量关系BD ＋CE =DE 是否始终成立,若成立,请证明,若不成立,请说明理由.

（08湖北恩施24题解析）六、(本大题满分12分)

24. 解:(1)?ABE∽?DAE, ?ABE∽?DCA 1分

∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°

∴∠BAE=∠CDA

又∠B=∠C=45°

∴?ABE∽?DCA 3分

(2)∵?ABE∽?DCA

∴

由依题意可知CA=BA=

∴

∴m= 5分

自变量n的取值范围为1<n<2. 6分

(3)由BD=CE可得BE=CD,即m=n

∵m=

∴m=n=

∵OB=OC= BC=1

∴OE=OD= －1

∴D(1－ , 0) 7分

∴BD=OB－OD=1-( －1)=2－ =CE, DE=BC－2BD=2-2(2－ )=2 －2

∵BD ＋CE =2 BD =2(2－ ) =12－8 , DE =(2 －2) = 12－8

∴BD ＋CE =DE 8分

(4)成立 9分

证明:如图,将?ACE绕点A顺时针旋转90°至?ABH的位置,则CE=HB,AE=AH,

∠ABH=∠C=45°,旋转角∠EAH=90°.

连接HD,在?EAD和?HAD中

∵AE=AH, ∠HAD=∠EAH-∠F=45°=∠EAD, AD=AD.

∴?EAD≌?HAD

∴DH=DE

又∠HBD=∠ABH+∠ABD=90°

∴BD +HB =DH

即BD ＋CE =DE 12分

7.（08湖北荆门）28．（本小题满分12分）

已知抛物线y=ax2+bx+c的顶点A在x轴上，与y轴的交点为B（0，1），且b=－4ac．

(1) 求抛物线的解析式；

(2) 在抛物线上是否存在一点C，使以BC为直径的圆经过抛物线的顶点A？若不存在说明理由；若存在，求出点C的坐标，并求出此时圆的圆心点P的坐标；

(3) 根据(2)小题的结论，你发现B、P、C三点的横坐标之间、纵坐标之间分别有何关系?